黄金分割法+斐波那契数列法求单峰函数极小值点

使用黄金分割法求极小值点。

前提：函数在所求区间为单峰函数，即存在唯一极小值点。

初步构思

单峰函数：

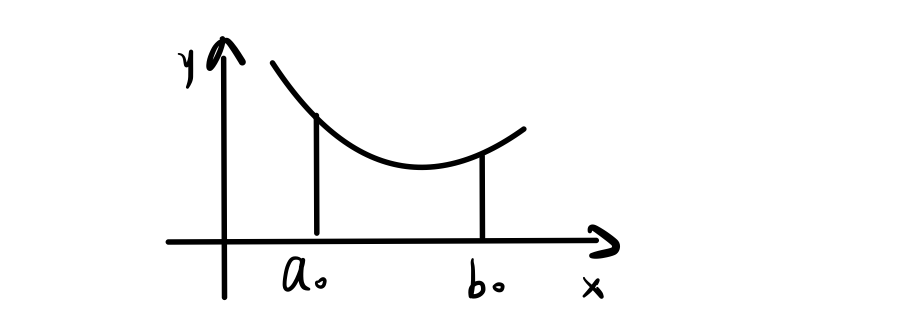可以使用对称压缩区间的方法，满足： \[a_1 - a_0 = b_0 - b_1 = \rho*(b_0-a_0)\]

其中： \[\rho < \frac {1} {2}\]

做上述处理后，可以得到点\(a_1\)和\(b_1\)

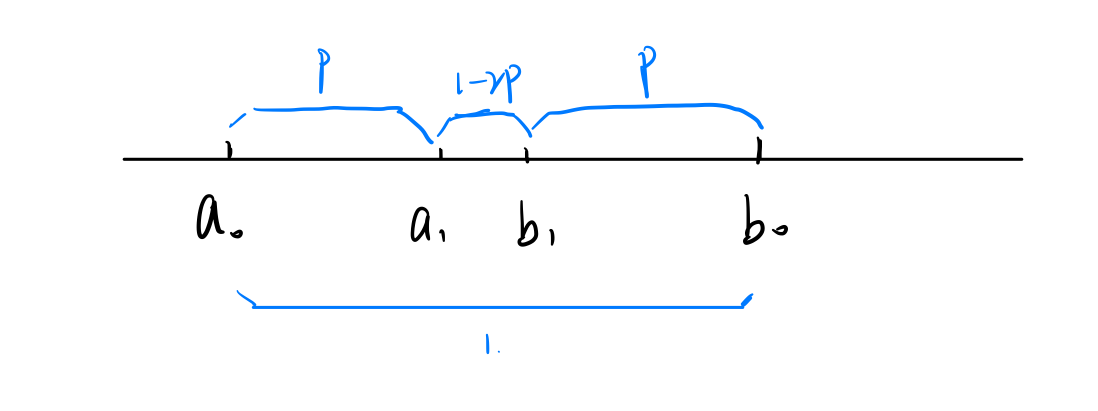
然后比较\(f(a_1)\)与\(f(b_1)\)的函数值大小

if \(f(a_1) < f(b_1)\) :

则函数的最小值落在区间\[[a_0,b_1]\]

重复上述的操作，可压缩出在一定精度区间范围内最小值点的值

黄金分割法

我们可以找到一个合适的\(\rho\)值，使得每次迭代只要计算一次目标函数的值。如图所示，这样的\(\rho\)满足\[\rho(b_1-a_0)=b_1-b_2\]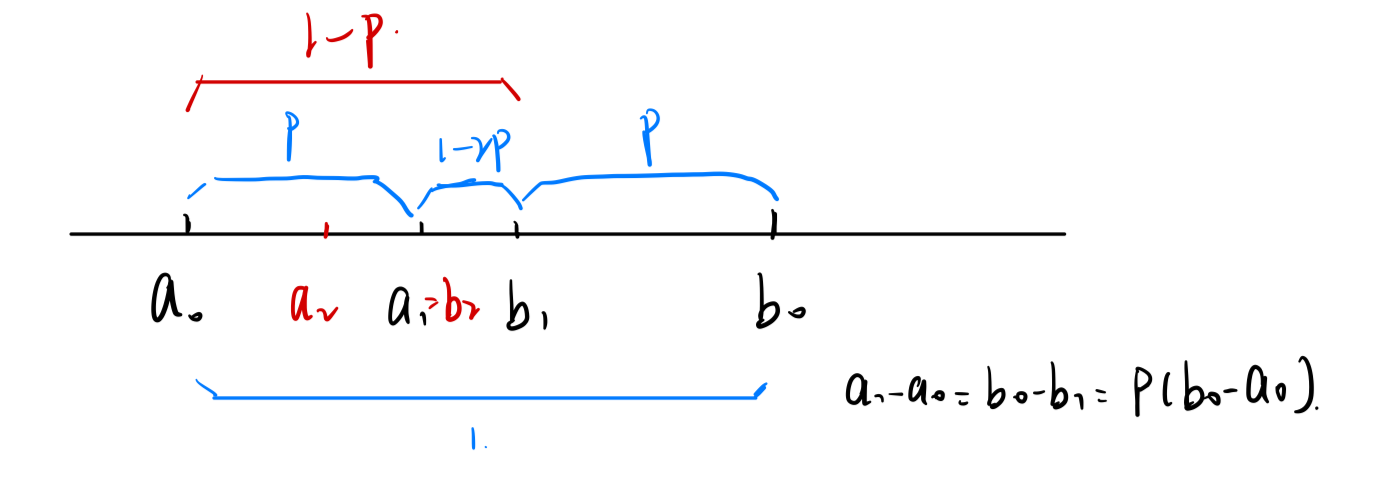

设区间\([a_0,b_0]\)为1，如图所示可得式子：\[\rho(1-\rho)=1-2\rho\]

要求\(\rho<\frac {1} {2}\),解的\[\rho=\frac {3-\sqrt 5 } {2}\]

此时，注意到\[1-\rho= \frac {\sqrt 5-1 } {2}\]

故有\[\frac {\rho} {1-\rho}=\frac {3-\sqrt 5 } {\sqrt 5-1}=\frac {\sqrt 5-1 } {2}=\frac {\sqrt 1-\rho } {1}\]

\[\frac {\rho} {1-\rho}=\frac {\sqrt 1-\rho } {1}\]

以\(\frac {\rho}{1-\rho}\)的比例划分区间，可以使得短区间与长区间之间的壁纸等于长区间与整个区间长度的比值

同时，在第N步的压缩后，极小值所在的区间长度为\[(1-\rho)^N \approx 0.61803)^N\]

以此可以估计迭代的次数

斐波那契数列法

在黄金分割法中，\(\rho\)的值在迭代过程中是固定的，如果迭代过程中动态调整\(\rho\)的的值，如图所示，可得

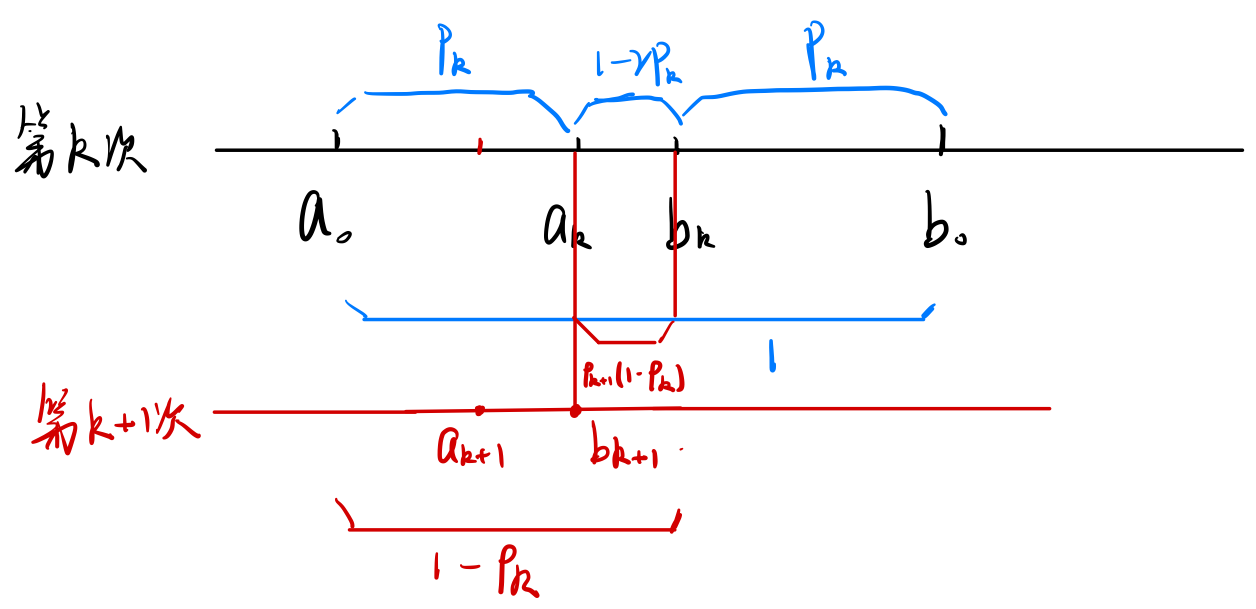
\[\rho_k+1(1-\rho_k)=1-2\rho_k\]

即\[\rho_{k+1} = 1- \frac {\rho_k } {1-\rho_k}\tag{1}\]

其总压缩比则变为\[(1-\rho_1)(1-\rho_2)...(1-\rho_n)\]

则我们的优化目标为使得总压缩比越小，其效率越高

引入斐波那契数列

对于斐波那契数列，令\(F_{-1}=0\),\(F_0=1\),有：

\[F_{k+1} = F_k + F_{k-1}\]